基于数组的序列：Python 动态数组原理与插入排序

根据教材 《数据结构与算法 Python 实现》 整理，代码和笔记可前往我的 Github 库下载 isKage/dsa-notes 。【建议 star !】

本文介绍了低层次数组的原理，并自定义实现了 Python 的一个动态数组。并详细分析了底层存储原理、摊销时间。分析了一些基于数组的案例，例如插入排序算法。同时指出了组成字符串和多维数组创建的常见误用。

1 Python 序列类型

Python 有各种序列类型，例如：内置的列表 list 、元组 tuple 和字符串 str 类

  • 这些序列类型支持用下标访间序列元素，如 A[i]
  • 这些类型均使用数组来表示序列
  • 一个数组即为一组相关变量，它们一个接一个地存在内存里的一块连续区域内

而 数组 Array 抽象数据类型为：

1
2
3
4
5
6
7
8
9
10
11
12
ADT Array{
	数据对象: A = {A1, A2, ..., An｝
	基本操作: 
		A.init(S): 使用序列 S 初始化数组 A
		len(A): 返回数组 A 的长度
		A.is_empty(): 检查数组 A 是否为空，如为空则返回 True
        A.get_item(n): 返回数组 A 的第 n 个元素
        A.locate(e): 返回数组 A 中第一个等于 e 的元素的位置
        A.insert(n, e): 在数组 A 的第 n 个元素前插入元素 e
        A.delete(n): 删除数组 A 的第 n 个元素
        A.clear(): 清空数组 A
} ADT Array

2 低层次数组

从计算机底层角度理解数组的存储方式：数组是一些变量一个接一个地存在内存里的一块连续区域内。例如：

对于这种连续的存储方式，索引变得十分迅速，例如上例：已知 'S' 的地址为 2146 而它位于位置 index = 0 那么索引 'L' 只要寻找地址 start + cellsize * index 即 2146 + 2 * 4 = 2154 即可找到 'L' 的地址。

从底层上理解数组，我们又可以分为：紧凑数组和引用数组

2.1 紧凑数组

一个存储基本元素（如字符）的数组，被称为紧凑数组。例如上面的例子存储的 SAMPLE 就是紧凑数组。

除了 Python 默认的紧凑数组，我们也可以利用 array 模块自定义紧凑数组。例如：

1
2
3
from array import array

x = array('i', [1, 2, 3, 4])

其中 'i' 参数代表以整型类型存储，这个会定义分配的空间，一般整型分配 2 or 4 个字节。其他类型例：

例如刚刚的例子 [1, 2, 3, 4] 以 'i' 即有符号整型存储，分配空间为一个元素 4 字节，可以使用 Python 的 id() 函数检查一下：

1
2
3
4
5
6
7
from array import array

x = array('i', [1, 2, 3, 4])
print(id(x[1]) - id(x[0]))
print(id(x[2]) - id(x[1]))
# 32
# 32

这里的 32 表示 32 个比特 bit ，而 8 bit = 1 byte 故二者之间确实相隔 4 字节，而且两两相隔 4 字节，说明是紧凑的。

对于 array 模块，我们只能定义它提供的数据类型的紧凑数组，即 i, f, d （整型、浮点型等），他们的内存大小已经确定。如果想完全自定义一个紧凑数组，同时还有满足底层数组的要求（动态数组），可以采用 ctypes 模块实现，见 [3.3 节：实现动态数组](###3.3 实现动态数组)。

2.2 引用数组

一个存储对象的引用的数组，被称为引用数组。例如：对于下面这个列表

1
['Rene', 'Joseph', 'Janet', 'Jonas', 'Helen', 'Virginia']

其存储方式如图，每个数组元素存储的是字符串数据的引用（地址）。不同于紧凑数组，存储不同类型的数据要分配的空间是不同的，而引用数组避免了这个困难。因为不同地址的大小是固定的，所以直接存储地址既能满足快速索引，又可以避免不同数据带来的分配空间难题。

而这也带了列表的某些特性，例如用下面的方法创建的列表，实则存储了各个数字的地址，而数字本身是不可变的常量。

1
primes = [2, 3, 5, 7, 11, 13, 17, 19]

此时如果有

1
temp = [7, 11, 13]

那么，temp 的这三个元素与 primes 的对应元素是相同的，因为他们都是存储了不可变常数 7, 11, 13 的地址。

1
2
3
4
5
6
primes = [2, 3, 5, 7, 11, 13, 17, 19]
temp = [7, 11, 13]
print(
    id(7) == id(primes[3]) == id(temp[0])
)
# True

3 动态数组和摊销

由之前的分析，我们发现：创建低层次数组时，必须明确声明数组的大小，以便系统为其存储分配连续的内存。

3.1 动态数组

不过 Python 提供了一个算法技巧，即动态数组。在 Python 中，创建一个列表，分配给这个列表的数组空间一般不与列表相同，而是更大。例如 [1, 2, 3] 列表的数组可能可以存储三个以上的元素。我们可以通过以下的代码验证：

1
2
3
4
5
6
7
8
import sys

data = []
for k in range(20):
    length = len(data)
    size = sys.getsizeof(data)
    print("数组大小: {}, 数组内存分配: {} Byte (字节)".format(length, size))
    data.append(None)

注意到，当数组为空时，仍然分配了 56 字节，对于 64 位 (bit) 操作系统，这一般意味着预留了 7 个元素的空间。

除此之外，而且当数组即将满时，Python 会自动创建一个更大的数组，并将原来的元素完全拷贝进新的数组。正如上图所示，当不断增加元素时，数组内存空间也在不断扩大。

3.2 摊销

对于不断扩大数组空间有两种策略：

  • 固定增量策略：每次数组大小增大一个常数
  • 翻倍增量策略：每次数组大小翻倍

首先，我们给出结论，实际 Python 采用的是第二种方式——翻倍增量策略，下面证明这样的策略摊销时间更短。

我们定义摊销时间为

T(n)n\frac{T(n)}{n} \notag

其中 nn 表示数组长度，而 T(n)T(n) 表示进行增量的总运行时间。

3.2.1 固定增量策略

假设每次在数组填满后，扩展 c 个空间。即每次增大的数量都是 c 的倍数，初始化了 k=nck = \frac{n}{c} 次数组（如果设从长度为 1 不断加 c 增加到 n 需要的次数为 k，那么 k 满足 k⋅c=nk\cdot c = n）。那么扩展到 n 这个长度需要操作：

n+c+2c+3c+⋯+kc=n+ck(k+1)/2n + c + 2c + 3c + \cdots + kc = n + ck(k+1)/2

c,2c,3c,⋯c, 2c, 3c, \cdots 代表每次需要初始化新增数组的长度，nn 代表复制次数。而 k∼nk \sim n ，故最后的总时间 T(n)∼O(n2)T(n) \sim O(n^2) 。那么摊销时间为 O(n)O(n) 。

3.2.2 翻倍增量策略

假设每次在数组填满后，翻倍自身的大小，初始化了 k=log⁡2nk = \log_2{n} 次数组（如果设从长度为 1 不断乘以 2 翻倍到 n 需要的次数为 k ，那么 k 满足 2k=n2^k = n）。那么扩展到 n 这个长度需要操作：

n+1+2+22+23+⋯+2k=n+2k+1−1=3n−1n + 1 + 2 + 2^2 + 2^3 + \cdots + 2^k = n + 2^{k+1} - 1 = 3n - 1

1,2,22,⋯1, 2, 2^2, \cdots 代表每次需要初始化新增数组的长度，nn 代表复制次数。故最后的总时间为 O(3n−1)=O(n)O(3n-1) = O(n) ，于是摊销时间为 O(1)O(1)。

  • 比较二者，翻倍增量策略更优，摊销时间复制度仅为 O(n)

很明显，从摊销时间来看，翻倍增量策略更优。直观地理解：摊销时间代表的是平均时间，而相比每次增加 c ，通过翻倍来达到长度 n 会更快。相当于通过不计空间成本的方式达到长度 n ，所以在平均来看，翻倍更优。

3.3 实现动态数组

当知道了 Python 底层如何构建数组后，我们可以使用 Python 的 ctypes 模块来自定义动态数组。我们希望它可以满足：

  • 初始化成立；
  • 紧凑的，可以快速索引；
  • 可以添加元素（添加元素的方法要满足动态数组）；
  • 针对添加元素，需要判断数组大小是否足够。如果不够，采用翻倍增量策略进行数组扩展；
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
import ctypes


class DynamicArray:
    """
    自定义实现动态数组，_ 开头表示非公有方法，不建议外部误调用
    """

    def __init__(self):
        """初始化空数组"""
        self._n = 0  # 数组实际元素个数
        self._capacity = 1  # 默认数组空间大小
        self._A = self._make_array(self._capacity)  # 创建大小为 _capacity 的数组

    def _make_array(self, c):
        """创建大小为 c 的数组"""
        return (c * ctypes.py_object)()

    def __len__(self):
        """返回数组元素个数"""
        return self._n

    def __getitem__(self, k):
        """索引数组第 k 个元素"""
        if not 0 <= k < self._n:
            raise IndexError('Invalid index')
        return self._A[k]

    def append(self, obj):
        """数组末尾添加元素"""
        if self._n == self._capacity:  # 判断数组空间
            self._resize(2 * self._capacity)  # 翻倍增量策略

        self._A[self._n] = obj  # 更新数组尾部元素
        self._n += 1  # 更新实际元素个数

    def _resize(self, c):
        """扩展数组大小"""
        B = self._make_array(c)  # 创建大小为 c 的新数组
        for k in range(self._n):
            # 拷贝原来数组元素
            B[k] = self._A[k]

        self._A = B  # 更新数组对象
        self._capacity = c  # 更新存储空间大小

    def __str__(self):
        """字符串重载，以字符串得到方式展示数组内容"""
        return "[" + ", ".join(str(self._A[i]) for i in range(self._n)) + "]"

    def get_memory_size(self):
        """返回数组的内存分配大小（字节）"""
        return self._capacity * ctypes.sizeof(ctypes.py_object)

通过下面的方式检查

1
2
3
4
5
6
7
8
array = DynamicArray()
for k in range(20):
    length = len(array)
    size = array.get_memory_size()
    print("数组大小: {}, 数组内存分配: {} Byte (字节)".format(length, size))
    array.append(k)

print(array) # [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19]

自定义动态数组的内存变化

从结果可知：每当数组实际元素达到内存分配的个数时，内存分配就会翻倍（即当 length=1,2,22,23,⋯length = 1, 2, 2^2, 2^3, \cdots 时内存就会乘以 2），这就是手动实现动态数组，采用翻倍增量策略的例子。

4 Python 列表和元组类的效率

4.1 不改变数组内容的操作

对于 Python 的列表和元组这两个序列类，不改变其内容的操作往往都是常量级别的时间复杂度 O(c)。例如：索引（因为是连续的内存空间，只需知道 index 计算即可得到对应的地址）、长度（因为在基类里保存了 __len__ 方法，可以直接调出）等。

不改变内容的操作

4.2 改变数组内容的操作

4.2.1 数组元素的插入 O(n)

将对象 o 插入到数组 A 的第 i 个元素前时（insert(o, i)）需要将后 n - i 个元素后移才能插入。最坏的情况就是插入到第 0 个位置，这样需要后移 n 个元素，即复杂度为 O(n) 。

  • 代码实现插入方法 insert
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class DynamicArray:
    ...
    
    def insert(self, obj, position):
    	"""在第 position 位置插入 obj"""
    	# 解决索引问题
        while position < 0:
            position += self._n
        position = position % self._n


        if self._n == self._capacity:
            # 空间不足
            self._resize(2 * self._capacity)  # 扩展

        for j in range(self._n, position, -1):
            # 后 n - position 向后移动一位
            self._A[j] = self._A[j - 1]

        self._A[position] = obj  # 更新第 position 位的元素
        self._n += 1  # 更新元素个数

4.2.2 数组元素的删除 O(n)

与插入元素相反，删除元素需要索引到对应元素，删去后需要将后面的元素向前移动一位。最坏的情况就是删除第一个元素，需要移动 n 个元素，复杂度为 O(n) 。

  • 代码实现删除方法 remove
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class DynamicArray:
    ...
    
	def remove(self, obj):
        """删除值 obj (不考虑重复)"""
        for k in range(self._n):
            if self._A[k] == obj:
                for j in range(k, self._n - 1):
                    # 前移
                    self._A[j] = self._A[j + 1]

            self._A[self._n - 1] = None  # help garbage collection
            self._n -= 1  # 更新个数
            return True
        raise ValueError('Value not found')  # 无匹配

实际上，Python 在删除元素后，也会动态调整空间大小，为简单期间，暂不手动实现。

4.2.3 改变数组内容的操作

针对这些会改变数组内容的操作，往往需要至少 O(n) 复杂度才能实现：

改变内容的操作

特别的，因为在末尾增加元素、插入元素、删除元素、在末尾删除元素、拼接等操作会带来存储空间的变化，所以可能需要扩展或缩小内存空间。故要考虑摊销的时间复杂度，这里采用的是翻倍增量策略的摊销（平均时间）为 O(1) 。

需要注意，摊销的 O(1) 代表的是平均时间，与一般的时间复杂度定义不同，一般时间复杂度考虑的是最坏情况。如果考虑最坏情况，则为 O(n) ，例如 append 最坏的情况需要 n 次，因为扩展空间后需要复制原来数组的 n 个元素。

5 Python 字符串类的效率

字符串的很多方面与列表和元组相同，这里主要介绍一个常见的【误用】。

5.1 组成字符串的误用

组成字符串

假设有一个很长的字符串对象 document ，我们的目标是构造一个新的字符串 letter ，该字符串仅包含 document 的所有字母。常见的误用为：

1
2
3
4
5
6
# 这是个错误的使用
letter = ""
for char in document:
    if char.isalnum():
        # 使用重载后的 + 进行组合
        letter += char

如果这样使用，每一次 letter = letter + char 都会创建一个新的对象 letter + char 并把它赋值给 letter 。假设 letter 最后长为 n ，那么需要进行近似 1+2+⋯+n1 + 2 + \cdots + n 次操作，复杂度为 O(n2)O(n^2) 。

5.2 正确使用

为了解决时间复杂度，我们可以用空间换时间，即不直接对 letter 操作，而是用一个临时的表 tmp 存储字符，然后在组成新的字符串 letter 。

1
2
3
4
5
6
7
tmp = []  # 临时表
for char in document:
    if char.isalpha():
        # append 操作平均为 O(1)
        tmp.append(char)
# 最后再组成字符串
letter = "".join(tmp)
  • 我们可以验证一下二者的速度：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import time

# 为验证，设置一个足够长的字符串
document = "hello world, welcome to Python :) Having a nice day! ...." * 10000

# 误用
letter = ""
start = time.time()
for char in document:
    if char.isalnum():
        # 使用重载后的 + 进行组合
        letter += char
end = time.time()
# print(letter)
print("直接组成消耗的时间: {}".format(end - start))

# 正确
tmp = []  # 临时表
start = time.time()
for char in document:
    if char.isalpha():
        # append 操作平均为 O(1)
        tmp.append(char)
# 最后再组成字符串
letter = "".join(tmp)
end = time.time()
# print(letter)
print("使用临时表消耗的时间: {}".format(end - start))

"""
直接组成消耗的时间: 3.8247530460357666
使用临时表消耗的时间: 0.07381105422973633
"""

6 插入排序算法

从第 2 个元素开始，比较它和之前的元素大小，如果它比前一个元素小，则接着往前比较，直到前一个元素小于它，则插入到这个元素的后面。（从小到大）

插入排序示意图

6.1 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def insertion_sort(arr):
    """
    从小到大排序数组
    :param arr: 数组
    :return: None
    """
    for i in range(1, len(arr)):
        # 从第 2 个元素开始
        current = arr[i]
        j = i

        while j > 0 and current < arr[j - 1]:
            # 当前一个元素不是第 0 个元素且比 current 大时
            arr[j] = arr[j - 1]  # 后移
            j -= 1  # 继续向前找

        # 插入
        arr[j] = current

6.2 算法分析

下面考虑的为从小到大排序

  • 最好的情况：已经是从小到大排序

此时只需要遍历第 2 个元素到最后一个元素即可，因为每次比较都发现比前一个元素大，没有插入操作。故复杂度为 O(n)O(n) 。

  • 最坏的情况：数组为从大到小排序

此时对第 i 个元素而言，都要插入到最前，前面的 i - 1 个元素均要后移一位，需要操作 i-1 + 1 （后移 i - 1 次，插入 1 次）。故对于从第 2 个元素开始遍历，需要次数 ∑i=2n (i−1+1)∼n2\sum\limits_{i=2}^n\ (i-1+1)\sim n^2 ，故复杂度为 O(n2)O(n^2) 。

所以，综合以上分析，插入排序的时间复杂度为 O(n2)O(n^2) 。

【注意】插入排序最坏情况才是 O(n2)O(n^2) ，而对于一些运气较好时，插入排序非常高效，可以对比选择排序。

6.3 与选择排序对比

每次从未排序的部分中选择最小的元素，将其放到前面已排序部分的末尾。（从小到大）

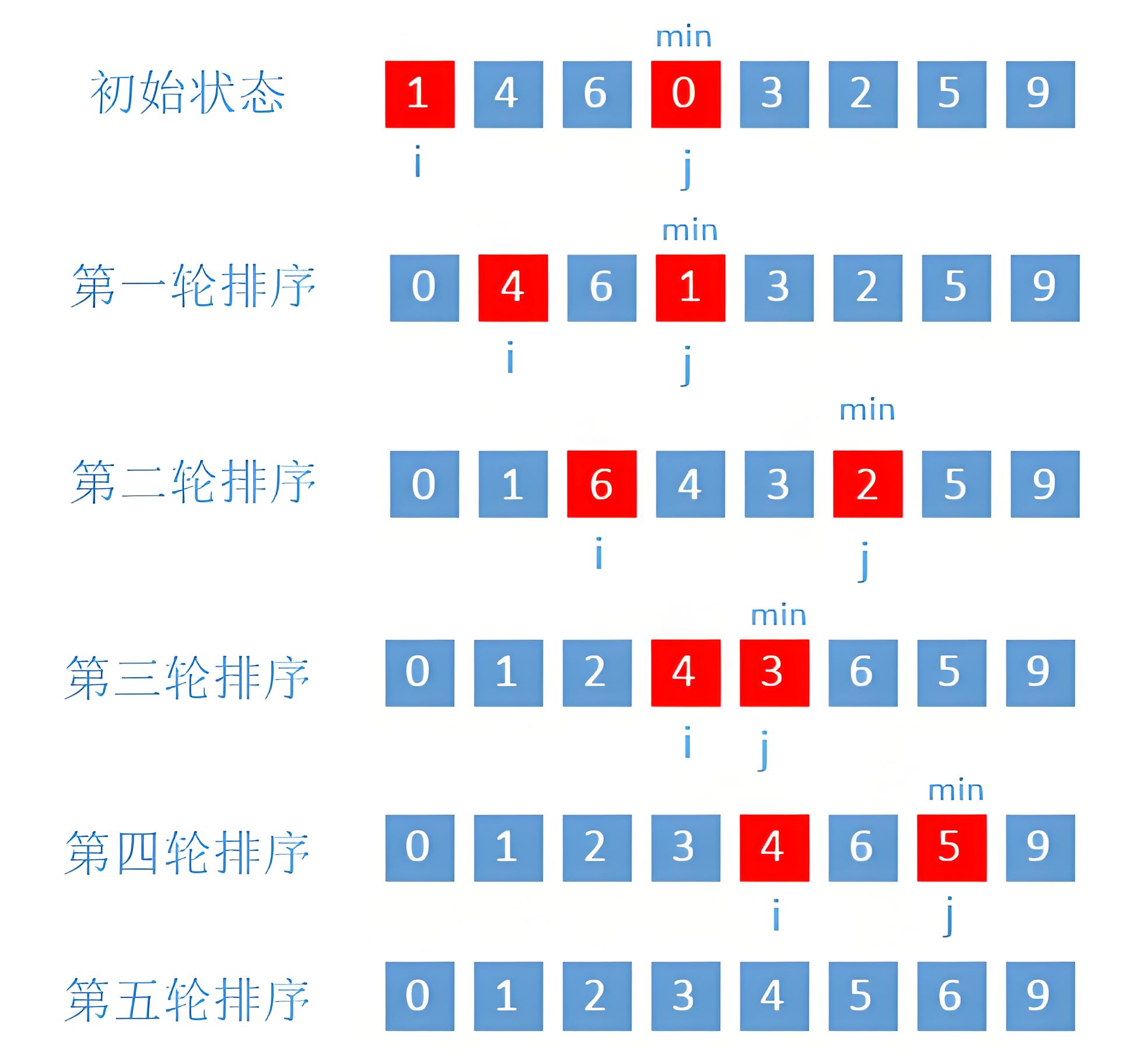
选择排序示意图

  • 选择排序的代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def selection_sort(arr):
    """
    选择排序：从小到大排序数组
    :param arr: 数组
    :return: None
    """
    for i in range(len(arr)):
        # 从起始开始遍历
        min_index = i
        for j in range(i + 1, len(arr)):
            if arr[j] < arr[min_index]:
                min_index = j  # 找到后面最小的元素
        
        # 将后面最小的元素放到前面子列的末尾
        arr[i], arr[min_index] = arr[min_index], arr[i]
  • 选择排序的算法分析

无论最好还是最坏（即无轮是从小到大还是从大到小排序的原数组），对于第 i + 1 个位置，选择排序都需要找到 i + 1 到 n 的最小元素，然后插入到第 i 个位置后。即使是从小到大排序好的原数组，都需要遍历以确定是否是最小元素。故复杂度为 ∑i=1n (n−i)∼n2\sum\limits_{i=1}^n\ (n - i) \sim n^2 即一定为 O(n2)O(n^2) 。

所以，【选择排序不如插入排序高效】。也可以通过下面的例子验证。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
x = [i for i in range(10000)]
start = time.time()
insertion_sort(x)
end = time.time()
print("insertion sort cost {}s".format(end - start))

x = [i for i in range(10000)]
start = time.time()
selection_sort(x)
end = time.time()
print("selection sort cost {}s".format(end - start))

"""
insertion sort cost 0.0012428760528564453s
selection sort cost 2.98787522315979s
"""

当遇见最好情况时，插入排序大约消耗了 0.0012 秒，而选择排序则消耗了 2.99 秒，是前者的 2492 倍！

7 多维数组的误用

7.1 误用

以创建二维数组（矩阵）为例，如果采用如下方式构建数组：【误用】

1
data = [[0] * n] * m

可以初始化一个列表，例如 m = 3, n = 6

1
2
3
4
5
6
m = 3
n = 6
data = [[0] * n] * m

# data = 
# [[0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0]]

但是此时 data 的第一维度的索引指向的是同一个列表对象，如图：

误用：指向同一列表对象

此时，如果改变 data[0][0] 的值，对应的 data[1][0] 和 data[2][0] 的值会一起变化（因为他们指向同一个列表对象，需要注意，被指向的列表对象 [0, 0, 0, 0, 0, 0] 这 6 个元素存储的是常数 0 的地址）。

1
2
3
4
5
data[0][0] = 1
print(data)

# data = 
# [[1, 0, 0, 0, 0, 0], [1, 0, 0, 0, 0, 0], [1, 0, 0, 0, 0, 0]]

7.2 正确使用

正确的创建方式：使用 Python 的列表推导式实例化新的列表对象

1
data = [[0] * n for _ in range(m)]

正确使用

1
2
3
4
5
6
7
8
m = 3
n = 6
data = [[0] * n for _ in range(m)]
data[0][0] = 1
print(data)

# data = 
# [[1, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0]]